Table of Contents

• Study Guide 8: Queuing Theory, File Systems
  • Queuing Theory
    • Concept Checks
  • File Systems
    • File Allocation Table (FAT)
      • FAT Index Structure
      • FAT Directory Structure
      • FAT Free Space Management
    • Fast File System (FFS)
      • FFS Index Structure
      • FFS Directory Structure
      • FFS Free Space Management
    • Concept Check
    • File Growth

Study Guide 8: Queuing Theory, File Systems

Queuing Theory

Concept Checks

Explain intuitively why response time is nonlinear with utilization. Draw a plot of utilization (x axis) vs. response time (y-axis) and label the endpoints on the x-axis.

Solution

Even with high utilization (99%), some of the time (1%), the server is idle, which is a waste. All this wasted time adds up, and in the steady state, the queue becomes very long. The graph should be linear-ish close to \(u = 0\) and grow asymptotically toward \(\infty\) at \(u = 1\).

If 50 jobs arrive at a system every second and the average response time for any particular job is 100ms, how many jobs are in the system (either queued or being serviced) on average at a particular moment? Which law describes this relationship?

Solution

\(50 jobs/s \times 0.1 s = 5 jobs\) (at any time). This is Little’s law - \(arrival-rate \times average-response-time = average-length-of-the-queue\).

Is it better to have N queues, each of which is serviced at the rate of 1 job per second, or 1 queue that is serviced at the rate of N jobs per second? Give reasons to justify your answer.

Solution

One queue that can process N jobs per second is faster (i.e the second option). Better response time (1 N sec vs 1 sec) and better utilization (no load-balancing problems), which gives you lower queuing delays on average.

What is the average queuing time for a work queue with 1 server, average arrival rate of \(\lambda\), average service time \(S\), and squared coefficient of variation of service time \(C\)?

Solution

Recall from definitions that we sometimes swap between symbols - \(S\) is another name for \(T_{ser}\). \(T_q = T_{ser}(\frac{u}{1-u})(\frac{C+1}{2})\) where \(u = \lambda T_{ser}\)

What does it mean if \(C = 0\)? What does it mean if \(C = 1\)?

Solution

If \(C = 0\), then your service rate is regular and deterministic, which means that tasks are completed at a constant rate. If \(C = 1\), then your arrivals can be modeled as a Poisson Process, and the interval between jobs being serviced can be modeled as an exponential distribution.

File Systems

A file system provides persistent, named data to the user. It is an abstraction layer maintained by the operating system to make it easy for users and programs to interact with files.

A file is a named collection of data in a file system. Files allow an arbitrary amount of data to be referred to by a single, meaningful name. A file is composed of two parts: metadata and data. The metadata contains information about a file needed by the operating system such as size, owner, and access control. The data is the actual content of the file that the user or program puts in. While this data can be interpreted as something meaningful using programs (e.g. text editors, PDF readers), the file system will view the data as simply a raw sequence of bytes.

A directory is a list of mappings from human readable file names to a specific underlying file or directory. When given a path to a file or directory, the process is a recursive procedure of reading directories and finding the correct mapping. Many file systems have support for two types of directory entries: hard and soft links. Hard links are directory entries that map different names to the same file number. This allows for one underlying file to have many different names. Hard links can’t span across multiple file systems since file numbers will differ across different file systems. They can be created using ln [target] [dest] command. On the other hand, soft links, also known as symbolic links, are directory entries that map a name to another name. These are commonly known as shortcuts. Since path names can be the same across multiple file systems, soft links can move across different file systems. They can be created using ln -s [target] [dest] command.

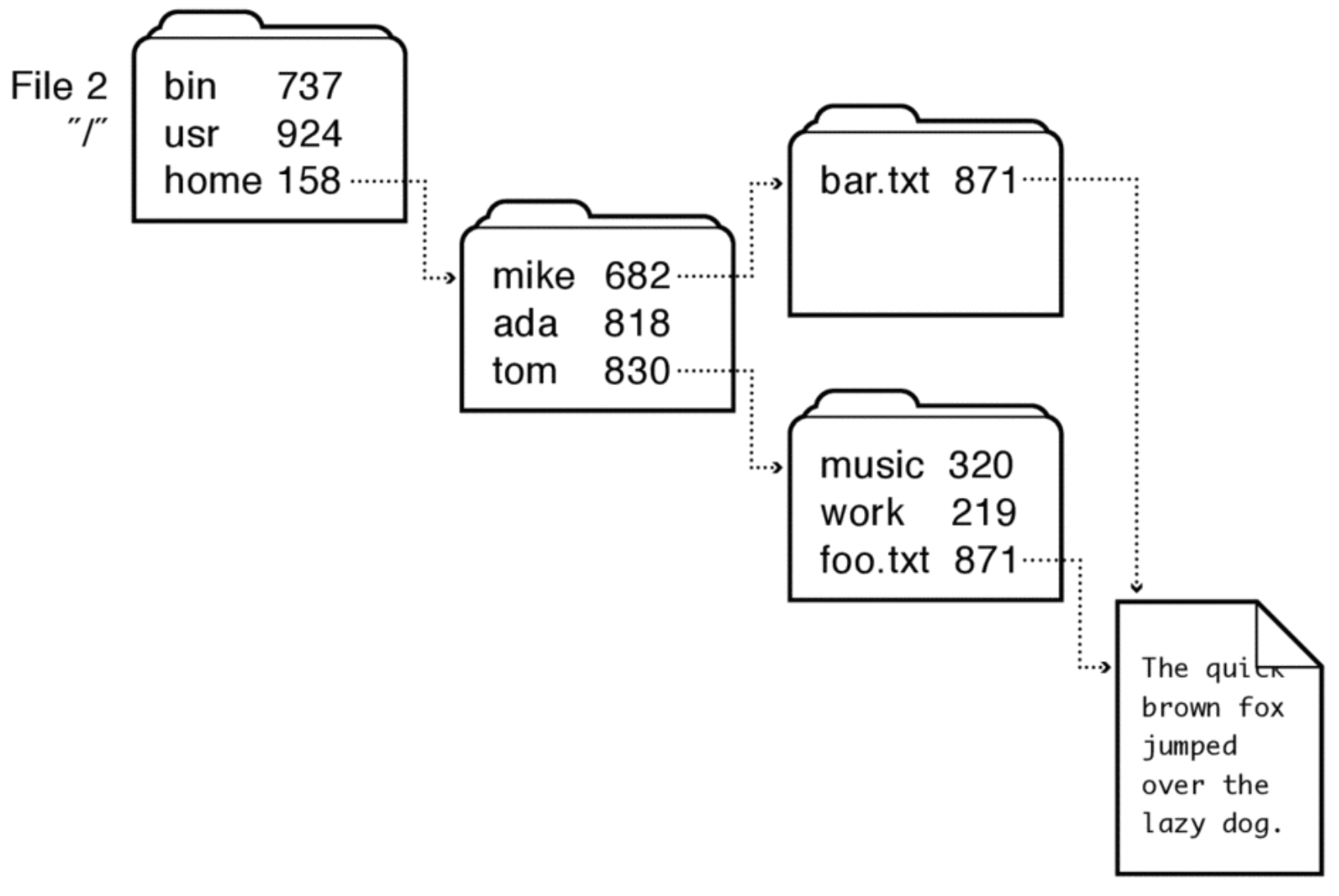
Figure 1: Hard Link

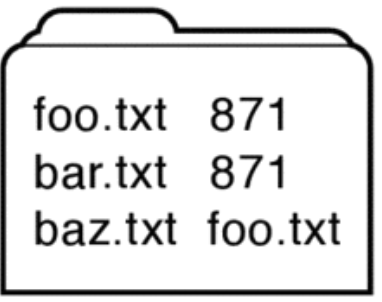
Figure 2: Soft Link

Throughout the file system unit, we will examine several file system implementations. The main components to focus are the index structure, directory structure, and free space tracking.

File Allocation Table (FAT)

File Allocation Table (FAT) is a file system developed by Microsoft in the 1970s.

FAT Index Structure

FAT file system is named after its index structure which is called the file allocation table, an array where each element corresponds to a disk block. Each file corresponds to a linked list of FAT entries containing a pointer to the next FAT entry. This means that each element N in FAT is an integer. This represents the index within the array of the next block within the file. The first few entries in the FAT array are reserved to store key data such as the boot sector, the array itself, and root directory. The index of the first entry of a file (i.e. the index that it starts at) is set to be the file number.

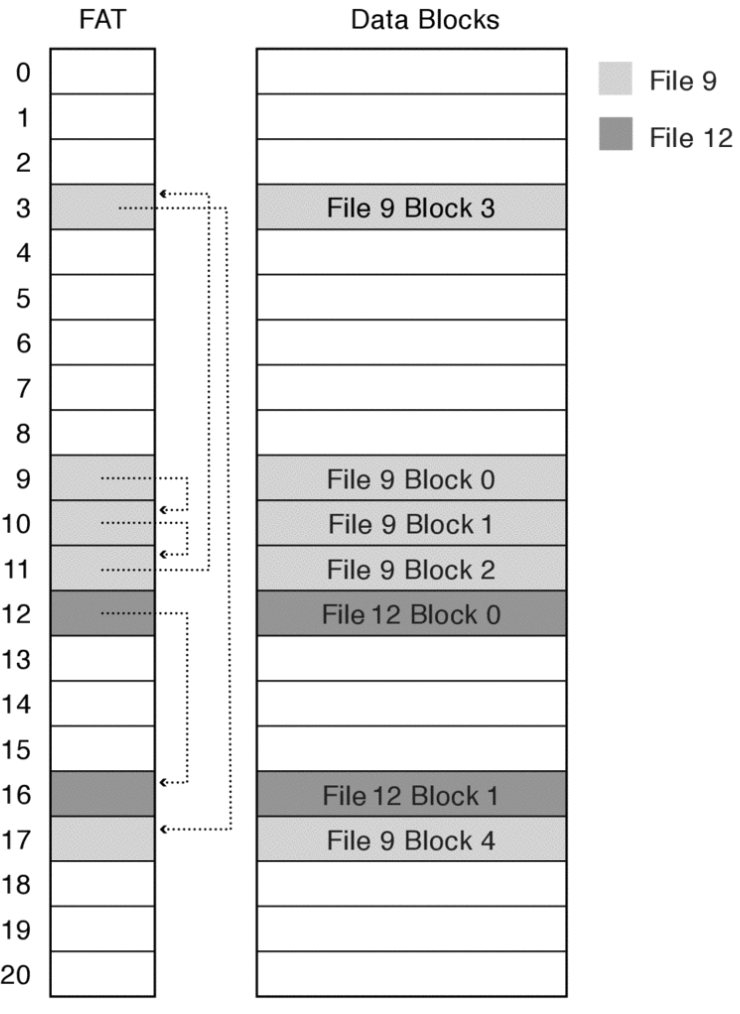
Figure 3: FAT

While no longer the default file system for Microsoft’s devices, FAT is still commonly found on many portable and embedded devices (e.g. digital cameras) due to its simplicity and support by many operating systems. However, the FAT file system suffers from bad random access performance since accessing a specific offset in a file requires traversing through the linked list. Moreover, file sizes are encoded in 32 bits, so no file can be larger than \(2^{32} - 1\) bytes (i.e. \(4 GiB\)).

FAT Directory Structure

Contrary to other file systems, the FAT file system is forced to store metadata as part of the directory entry rather than in the FAT entry itself since the FAT entry doesn’t have any space; it’s merely a 32-bit integer as discussed earlier. As a result, each file can be accessed via exactly one directory entry, meaning there can’t be any hard links.

FAT Free Space Management

The FAT file system uses the FAT array for free space tracking as well. If the entry of a FAT array is 0, it marks a free entry. When allocating a new file or an additional block for an existing file, the file system will walk through the FAT array to find a zero entry. As a result, allocation of multiple sectors may take a long time. Furthermore, disk blocks within one file may be spread across far-apart disk blocks instead of being placed sequentially, which reduces disk performance.

Fast File System (FFS)

The Berkeley Fast File System (FFS), also called the BSD Fast File System, emphasizes the importance of accessing a file’s blocks quickly while also maintaining good disk performance. It maintains good performance for both small and large files.

FFS Index Structure

FFS uses a fixed, asymmetric tree called a multi-level index. Each index is rooted at an inode that stores the file’s metadata and pointers to data. It’s important to note that an inode does not store the file’s name or any actual data in the inode itself. Inodes are stored in a fixed block on disk in an inode array.

Pointers come in different forms, but they’re just block numbers. Direct pointers point directly to the block, meaning the pointer is a block number of a block that contains the file’s data. An indirect pointer points to an indirect block which is an array of direct pointers. An indirect block is just a block (i.e. raw bytes) which we just interpret as an array of unsigned integers; there is nothing special about an indirect block compared to any other block on disk. Similarly, a double indirect pointer points to a double indirect block which contains an array of indirect pointers. The levels of indirect pointer continue (i.e. triple, quadruple), but you will typically see up to triple indirect pointers.

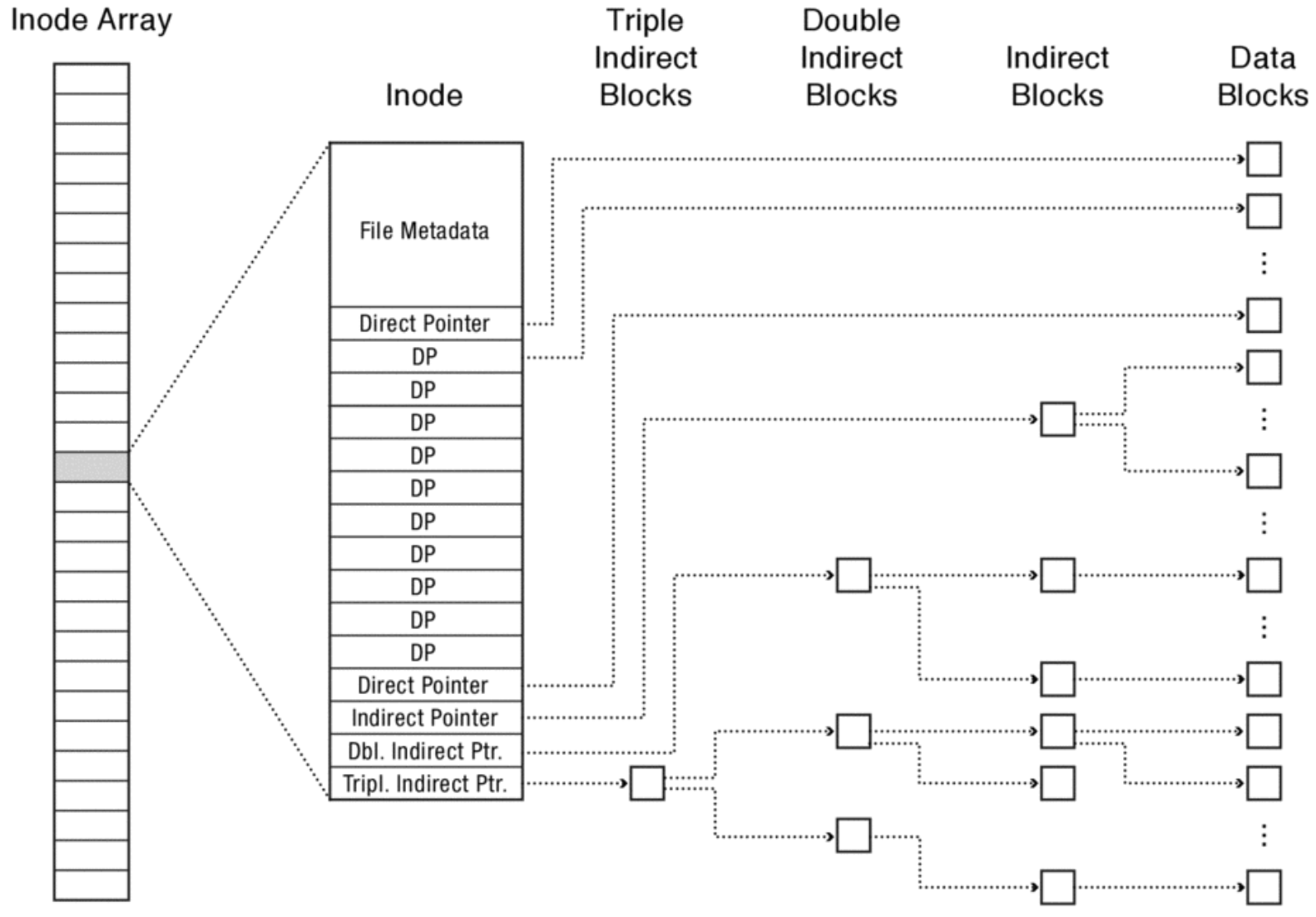
Figure 4: Inode

FFS Directory Structure

The index of an inode in this inode array is called the inumber, which FFS uses as the file number as well. Directories will map a file name to an inumber. Unlike FAT, the metadata of a file is now stored in the inode itself, not the directory entry. As a result, FFS supports hard links.

FFS Free Space Management

To track free space, FFS allocates a bitmap, where each bit indicates whether the block corresponding to that bit is free. This bitmap is stored on a fixed place in disk. Unlike FAT, FFS will optimize disk performance using block group placement which places a file’s inode block and data block near each other. Moreover, it will reserve a fraction of the disk’s space (e.g. 10%), showing a reduced capacity to the user. This is important because the block group placement relies on there being enough free space on the disk.

Concept Check

What does it mean to format a FAT file system? Approximately how many bytes of data need to be written in order to format a 2 GiB flash drive (with 4 KiB blocks and a FAT entry size of 4 bytes) using the FAT file system?

Solution

Formatting a FAT file system means resetting the file allocation table (mark all blocks as free). The actual data can be zero-ed out for additional security, but it is not required. Formatting a 2 GiB FAT volume will require resetting \(2^{19}\) FAT entries, which will involve approximately \(2^{21} bytes = 2 MiB\).

Your friend who has never taken an Operating Systems class wants to format their external hard drive with the FAT32 file system. The external hard drive will be used to share home videos with your friend’s family. Give one reason why FAT32 might be the right choice. Then, give one reason why your friend should consider other options.

Solution

FAT32 is supported by many different operating systems, which will make it a good choice for compatibility if it needs to be used by many users. However, FAT32 has a 4GiB file size limit, which may prevent your friend from sharing large video files with it.

Consider an inode-based file system with 2 KiB blocks and 32-bit disk and file block pointers. Each inode has 12 direct pointers, an indirect pointer, a double indirect pointer, and a triple indirect pointer. How large of a disk can this file system support? What is the maximum file size?

Solution

A 32-bit disk pointer means there can be at most \(2^{32}\) blocks, so the maximum disk size this file system can support is:

\[2^{32} \times 2^{11} = 2^{43} = 8 TiB\]

The maximum file size is the block size multiplied by the number of all direct pointers (i.e. including the ones from the indirect pointers). We see that there are \(2048/4 = 512\) pointers per block. Therefore, the maximum file size is:

\(2048 \times (12 + 512 + 512^2 + 512^3)\) \(= 2^{11} \times (2^2 \times 3 + 2^9 + 2^{9 \times 2} + 2^{9 \times 3})\) \(= 2^{13} \times 3 + 2^{20} + 2^{29} + 2^{38}\) \(= 24 KiB + 513 MiB + 256 GiB\)

The last term dominates here, so the maximum file size is essentially 256 GiB.

From a software perspective, explain how an operating system reads a file like D:\My Files\Video.mp4 from a FAT volume.

Solution

First, the operating system must know that the FAT volume is mounted as D:\. It looks at the first data block on the FAT volume, which contains the root directory, and searches for the My Files subdirectory. If necessary, the root directory listing might occupy many blocks, and the operating system will follow the pointers in the FAT to scan through the entire root directory. Once the subdirectory entry for My Files is found, the operating system searches the subdirectory’s listing the Video.mp4 file. Once it knows the block number for the file, it can begin reading the file sequentially by following the pointers in the FAT.

Compare bitmap-based allocation of blocks on disk with a free block list.

Solution

Bitmap based block allocation is fixed size proportional to the size of the disk. This means wasted space when the disk is full. A free block list shrinks as space is used up, so when the disk is full, the size of the free block list is tiny. However, contiguous allocation is easier to perform with a bitmap. Most modern file systems use a free block bitmap, not a free block list.

For inode-based file systems, what is the point of having direct pointers? Why not just have indirect pointers since they can point to much more data than a single direct pointer?

Solution

As seen from the empirical study of file sizes, most files are small enough to be contained within the given direct pointers of an inode-based file system. Direct pointers are faster compared to indirect pointers since they need to read in less blocks to get to the underlying data block.

List the set of disk blocks that must be read into memory in order to read the file /home/csc4103/pintos.bean in its entirety from a UNIX BSD 4.2 file system (10 direct pointers, an indirect pointer, a double indirect pointer, and a triple indirect pointer) on a magnetic disk with 1 KiB block size. The /home/csc4103/pintos.bean file is 15,234 bytes. Assume that the directories in question all fit into a single disk block each and the inode array is resident in memory (i.e. don’t count inode array disk accesses).

Solution

1. Read in inode for root directory.
2. Read in block pointed to by the the first direct pointer for root inode.
3. Read in inode for home directory.
4. Read in block pointed to by the the first direct pointer for home inode.
5. Read in inode for csc4103 directory.
6. Read in block pointed to by the first direct pointer for csc4103 inode.
7. Read in inode for pintos.bean file.
8. -17 Read in each block pointed to by the each direct pointer for pintos.bean inode. This will read through \(1024 \times 10 = 10,240\) bytes of the file.
9. Since we still have \(15,234 - 10,240 = 4,994\) bytes remaining, we need to read in the indirect pointer for the pintos.bean inode.
10. -23 Read in direct blocks corresponding to the first five direct pointers in the indirect block read in from the previous step. Five direct pointers point to \(1024 \times 5 = 5120\) bytes, so the fifth block read in will only be partially full.

File Growth

In this question, we will explore how to grow a file in PintOS. This will be very similar to one of your tasks in possible later project. In PintOS, struct inode_disk from src/filesys/inode.c represents an inode. Let’s examine a modified struct inode_disk with 12 direct pointers and an indirect pointer.

#define BLOCK_SECTOR_SIZE 512
typedef uint32_t block_sector_t;
struct inode_disk {
    block_sector_t direct[12];  /* Direct pointers */
    block_sector_t indirect;    /* Indirect pointer */
    off_t length;               /* File size in bytes. */
    uint32_t unused[114];       /* Not used. */
};

What is the purpose of the unused member in struct inode_disk?

Solution

Each inode must be of size equivalent to the block size. The direct pointers, indirect pointer, and size only take up:

\[4 \times (12 + 1 + 1) = 56 bytes\]

As a result, we need to pad the rest of the struct with \(512-56 = 456\) bytes, or equivalently an array of 114 32-bit integers.

What is the maximum file size supported by this file system?

Solution

There are \(512/4 = 128\) direct pointers in an indirect block, so the maximum file size is:

\(512 \times (12 + 128) = 2^9 \times (2^2 \times 3 + 2^7)\) \(= 2^{10} \times (2 \times 3 + 2^6)\) \(= 70 KiB\)

What data structure should you use to represent an indirect block?

Solution

Since an indirect block is an array of direct pointers, block_sector_t[128] would be adequate.

Implement inode_resize to grow or shrink the inode based on the given size. If the resize operation fails for any reason, the inode should be unchanged and the function should return false. Assume unallocated block pointers have value 0.

/* Allocates a disk sector and returns its number. */
block_sector_t block_allocate(void);
/* Frees disk sector N. */
void block_free(block_sector_t n);
/* Reads contents of disk sector N into BUFFER. */
void block_read(block_sector_t n, uint8_t buffer[512]);
/* Write contents of BUFFER to disk sector N. */
void block_write(block_sector_t n, uint8_t buffer[512]);

bool inode_resize(struct inode_disk* id, off_t size) {
    block_sector_t sector;
    /* Handle direct pointers. */
    for (int i = 0; i < 12; i++) {
        if (size <= BLOCK_SECTOR_SIZE * i && id->direct[i] != 0) {
            /* Shrink. */
            ________________________________;
            ________________________________;
        } else if (size > BLOCK_SECTOR_SIZE * i && id->direct[i] == 0) {
            /* Grow. */
            ________________________________;
        }
    }
    /* Check if indirect pointers are needed. */
    if (id->indirect == 0 && size <= 12 * BLOCK_SECTOR_SIZE) {
        id->length = size;
        return true;
    }
    block_sector_t buffer[128];
    memset(buffer, 0, 512);
    if (id->indirect == 0) {
        /* Allocate indirect block. */
        ________________________________;
    } else {
        /* Read in indirect block. */
        ________________________________;
    }
    /* Handle indirect pointers. */
    for (int i = 0; i < 128; i++) {
        if (size <= (12 + i) * BLOCK_SECTOR_SIZE && buffer[i] != 0) {
            /* Shrink. */
            ________________________________;
            ________________________________;
        } else if (size > (12 + i) * BLOCK_SECTOR_SIZE) && buffer[i] == 0) {
            /* Grow. */
            ________________________________;
        }
    }
    if (size <= 12 * BLOCK_SECTOR_SIZE) {
        ________________________________;
        ________________________________;
    } else {
        ________________________________;
    }
    id->length = size;
    return true;
}

Solution

bool inode_resize(struct inode_disk* id, off_t size) {
    block_sector_t sector;
    /* Handle direct pointers. */
    for (int i = 0; i < 12; i++) {
        if (size <= BLOCK_SECTOR_SIZE * i && id->direct[i] != 0) {
            /* Shrink. */
            block_free(id->direct[i]);
            id->direct[i] = 0;
        } else if (size > BLOCK_SECTOR_SIZE * i && id->direct[i] == 0) {
            /* Grow. */
            id->direct[i] = block_allocate();
        }
    }
    /* Check if indirect pointers are needed. */
    if (id->indirect == 0 && size <= 12 * BLOCK_SECTOR_SIZE) {
        id->length = size;
        return true;
    }
    block_sector_t buffer[128];
    memset(buffer, 0, 512);
    if (id->indirect == 0) {
        /* Allocate indirect block. */
        id->indirect = block_allocate();
    } else {
        /* Read in indirect block. */
        block_read(id->indirect, buffer);
    }
    /* Handle indirect pointers. */
    for (int i = 0; i < 128; i++) {
        if (size <= (12 + i) * BLOCK_SECTOR_SIZE && buffer[i] != 0) {
            /* Shrink. */
            block_free(buffer[i]);
            buffer[i] = 0;
        } else if (size > (12 + i) * BLOCK_SECTOR_SIZE) && buffer[i] == 0) {
            /* Grow. */
            buffer[i] = block_allocate();
        }
    }
    if (size <= 12 * BLOCK_SECTOR_SIZE) {
        /* We shrank the inode such that indirect pointers are not required. */
        block_free(id->indirect);
        id->indirect = 0;
    } else {
        /* Write the updates to the indirect block back to disk. */
        block_write(id->indirect, buffer);
    }
    id->length = size;
    return true;
}

How would you modify your solution to the previous question to handle sector allocation failures (i.e. disk runs out of space)?

Solution

Any time a new sector is allocated using block_allocate, you should add a check that resembles the following.

sector = allocate_block();
if (sector == 0) {
    inode_resize(id, id->length);
    return false;
}