Table of Contents

More Warmup

Vector and Matrix Norms

In lecture (and in previous assignments) we introduced the formal definition of vector spaces as a motivation for the interface and functionality of our Vector class. But besides the interface syntax, our Vector class needs to also support the semantics. One of the properties of a vector space is associativity of the addition operation, which we are going to verify experimentally in this assignment.

We have previously defined and used the function

double two_norm(Vector const&  x);

prototyped in work/include/matrix_operations.hpp and defined in work/src/matrix_operations.cpp.

In your source directory is a file norm_order.cpp that is the driver for this problem. It currently creates a Vector v and then invokes versions of two_norm on it four times, checking the results against that obtained by the first invocation.

The first invocation of two_norm is saved to the value norm0. We invoke two_norm a second time on v and save that value to norm1. We then check that norm0 and norm1 are equal.

As the program is delivered to you it also invokes two_norm_r on v and two_norm_s on v(for “reverse” and “sorted”, respectively). The program also prints the absolute and relative differences between the values returned from two_norm_r and two_norm_s with the sequential two_norm to make sure the returned values are the same. The functions two_norm_r and two_norm_s are defined in work/src/matrix_operations.cpp.

Absolute and relative differences are computed this way:

if (norm2 != norm0) {
    std::println("Absolute difference: ", std::abs(norm2 - norm0));
    std::println("Relative difference: ", std::abs(norm2 - norm0) / norm0);
}

(This is for norm2- the code for the others should be obvious.)

Modify the code for two_norm_r in work/src/matrix_operations.cpp so that it adds the values of v in reverse of the order given. I.e., rather than looping from 0 through num_rows()-1, loop from num_rows()-1 to 0.

The use of size_t

In almost all of the for loops we have been using in this course, I have written them using a size_t:
for (size_t i = 0; i < x.num_rows(); ++i) {
    // ...
}     
In C++ a size_t is unsigned and large enough to be able to index the largest thing representable in the system it is being compiled with. For all intents and purposes that means it is an unsigned 64-bit integer. Be careful if you are going to use a size_t to count down. What happens with the following code, for example:
int main() {
    size_t i = 1;
    assert(i > 0);
    i = i - 1;       // subtract one from one
    assert(i == 0);
    i = i - 1;       // subtract one from zero
    assert(i < 0);
    return 0;
}     
Do you expect all the assertions to pass? Do they?

Modify the code for two_norm_s in work/src/matrix_operations.cpp so that it adds the values of v in ascending order of its values. To do this, make a copy of v and sort those values using std::sort as follows:
Vector w(v);  // w is a copy of v    
std::sort(&w(0), &w(0) + w.num_rows());  
What happens when you run norm_order? Are the values of norm2 and norm3 equal to norm0? Note that the program takes a command line argument to set the max size of the vector. The default is 1M elements.

Answer the following questions in results/answers.md:

At what problem size (in terms of the number of elements in the Vector) do the answers between the computed norms start to differ?

How do the absolute and relative errors change as a function of problem size?

Does the Vector class behave strictly like an algebraic vector space?

Do you have any concerns about this kind of behavior?

Exercises

Parallel Norm

For this problem we are going to explore parallelizing the computation oftwo_norm in a variety of different ways in order to give you some hands on experience with several of the common techniques for parallelization. Each of the programs below consists of a header file for your implementation, a driver program, and a test program. The driver program runs the norm computation over a range of problem sizes, over a range of parallelizations. It also runs a sequential base case. It prints out GFlop/s for each problem size and for each number of threads. It also prints out the relative error between the parallel computed norm and the sequential computed norm.

Block Partitioning + Threads

Recall the approach to parallelization outlined in the lectures. The first step is to find concurrency – how can we decompose the problem into independent (ish) pieces and then (second step) build an algorithm around that?

The first approach we want to look at with norm is to simply separate the problem into blocks. Computing the sum of squares of the first half (say) of a vector can be done independently of the second half. We can combine the results to get our final result.

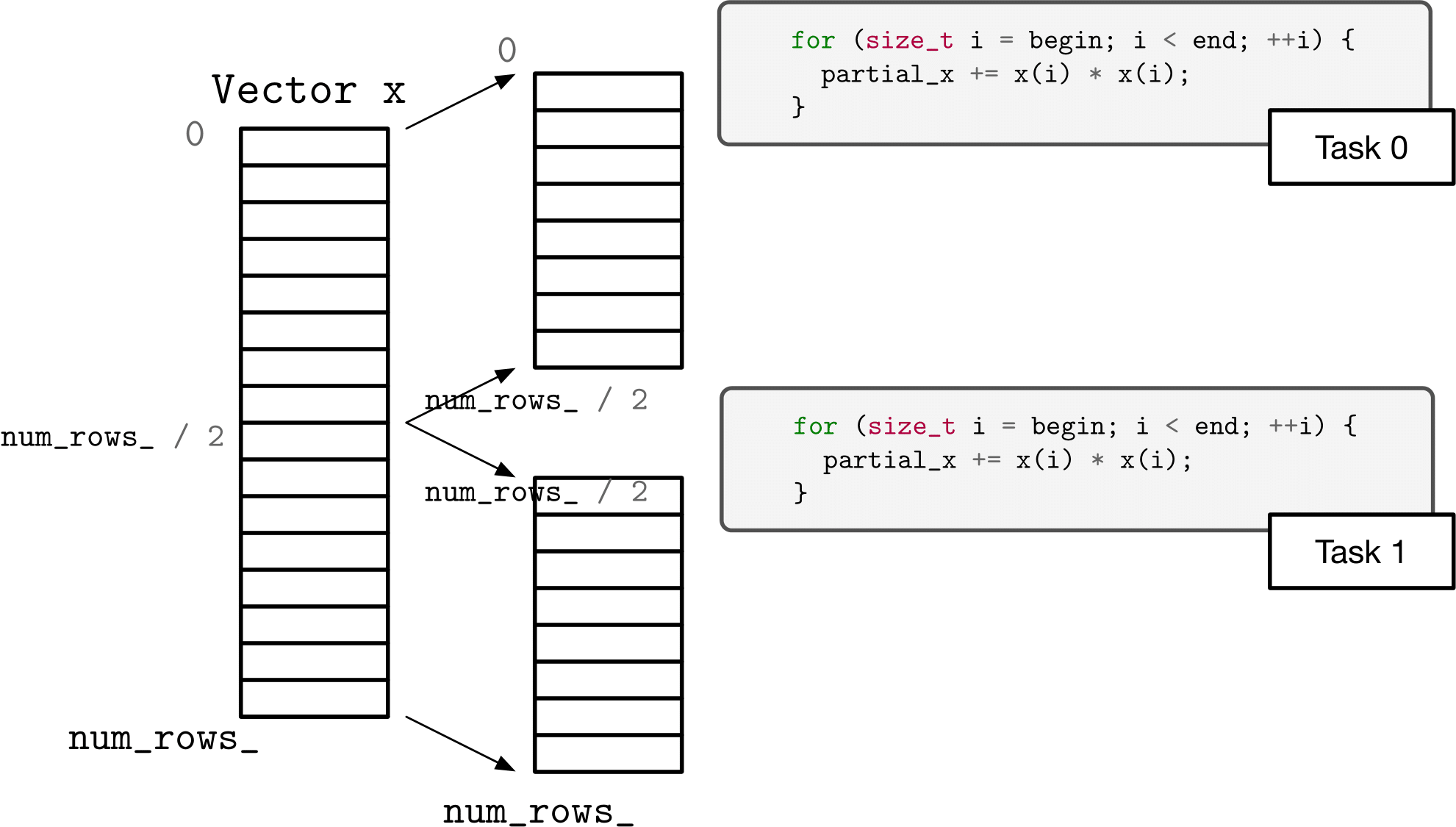
The program work/more_warmup/pnorm.cpp is a driver program that calls the function partitioned_two_norm_a in the file work/more_warmup/pnorm.hpp. The program as provided uses C++ threads to launch workers, each of which executes a specified block of the vector – from begin to end. Unfortunately, the program is not correct – more specifically, there is a race that causes it to give the wrong answer.

Fix the implementation of partitioned_two_norm_a in work/more_warmup/pnorm.hpp so that it no longer has a race and so that it achieves some parallel speedup. (Eliminating the race by replacing the parallel solution with a fully sequential solution is not the answer I am looking for.)

Answer the following questions in results/answers.md:

What was the data race?

What did you do to fix the data race?

Explain why the race is actually eliminated (rather than, say, just made less likely).

How much parallel speedup do you see for 1, 2, 4, and 8 threads?

Block Partitioning + Tasks

We presented in lecture related to concurrent programming that it was preferred to use tasks over using threads – to think in terms of the work to be done rather than orchestrating the worker to do the work. The program work/more_warmup/fnorm.cpp is the driver program for this problem. It calls the functions partitioned_two_norm_a and partitioned_two_norm_b, of which skeletons are provided in work/more_warmup/fnorm.hpp.

Complete the function partitioned_two_norm_a in work/more_warmup/fnorm.hpp, using std::async to create futures. You should save the futures in a vector and then gather the returned results (using get) to get your final answer. Use std::launch::async as your launch policy. The skeletons in work/more_warmup/fnorm.hpp suggest using helper functions as the tasks, but you can use lambdas or function objects if you like.

Once you are satisfied with partitioned_two_norm_a, copy it verbatim to partitioned_two_norm_b in work/more_warmup/fnorm.hpp and change the launch policy from std::launch::async to std::launch::deferred.

Answer the following questions in results/answers.md:

How much parallel speedup do you see for 1, 2, 4, and 8 threads for partitioned_two_norm_a?

How much parallel speedup do you see for 1, 2, 4, and 8 threads for partitioned_two_norm_b?

Explain the differences you see between partitioned_two_norm_a and partitioned_two_norm_b.

Cyclic Partitioning + Your Choice

Another option for decomposing the two norm computation is to use a “cyclic” or “strided” decomposition. That is, rather than each task operating on contiguous chunks of the problem, each task operates on interleaved sections of the vector.

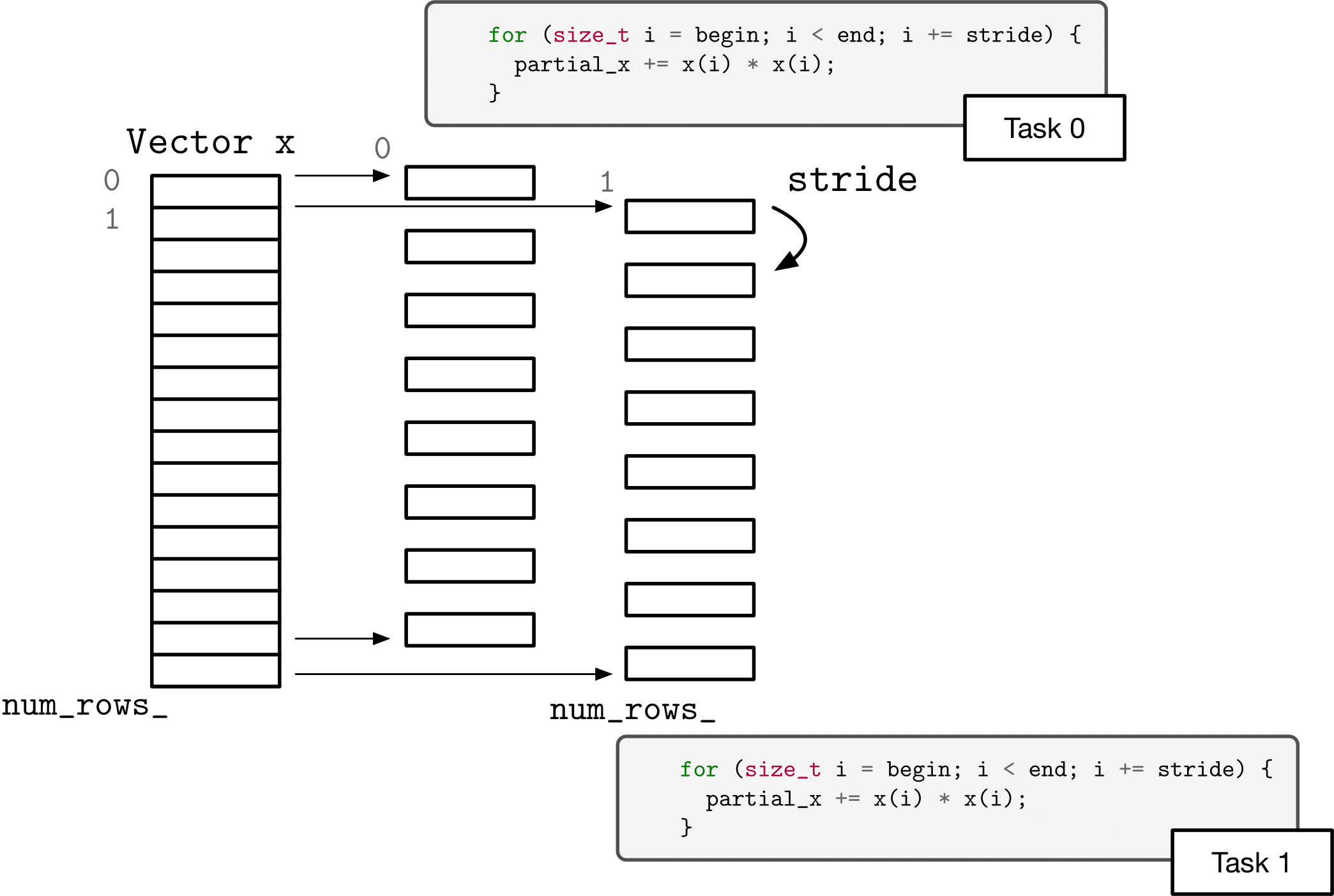
Complete the body of cyclic_two_norm in work/more_warmup/cnorm.hpp. The implementation mechanism you use is up to you (threads or tasks). You can use separate helper functions, lambdas, or function objects. The requirements are that the function parallelizes according to the specified number of threads, that it uses a cyclic partitioning (strides), and that it computes the correct answer (within the bounds of floating point accuracy).

Answer the following questions in results/answers.md:

How much parallel speedup do you see for 1, 2, 4, and 8 threads?

How does the performance of cyclic partitioning compare to blocked?

Explain any significant differences, referring to, say, performance models or CPU architectural models.

Divide and Conquer + Tasks

Another approach to decomposing a problem – particularly if you can’t (or don’t want to) try to divide it into equally sized chunks all at once – is to “divide and conquer.” In this approach, our function breaks the problem to be solved into two pieces (“divide”), solves the two pieces, and then combines the results. The twist is that to solve each of the two pieces (“conquer”), the function calls itself.

Recursion

Having a function call itself does not seem like a huge conceptual problem. But if we think about this in terms of defining what the function means, it introduces some problems. In the functional programming world, “programs” are simply functions and are analyzed mathematically. So in that framework, a program that calls itself is a function that is defined in terms of itself.

For example, we could define a function of \(f(x)\) in the following way
\[f(x) = x \times f(x-1)\]
What is \(f\) in a definition like this? Well, it depends on what \(f\) is. And, what do we get when we plug in a value for x, say, 3?
\[{rcl}f(3) = 3 \times f(2) = 3 \times 2 \times f(1) = 3 \times 2 \times 1 \times f(0) = \ldots\]
To make a self-referential definition sensible we have to define a specific value for the function with some specific argument (this is usually called the “base case”). In this example, we could define \(f(0) = 1\). Then the function is defined as:
\[f(x) = \left\{ \begin{array}{l} 1 \textrm{ if } x = 0 \\ x \times f(x-1) \textrm{ otherwise} \end{array}\right.\]
Recursion is a powerful abstraction tool. In the above example, we don’t define what \(f(x)\) is. Rather we define it as \(x\) times \(f (x - 1)\) – that is, we are abstracting away the computation – we are pretending that we know the value of \(f (x - 1)\) when we compute the value of \(f(x)\). To see what we mean, suppose we want to take the sum of squares of the elements of a vector (as a precursor for computing the Euclidean norm, say) using a function sum_of_squares. Well, we can abstract that away by pretending we can compute the sum of squares of the first half of the vector and the sum of squares of the second half of the vector. And, we abstract that away by saying we can compute those halves by calling sum_of_sqares.
double sum_of_squares(Vector const& x, size_t begin, size_t end) {
    return sum_of_squares(x, begin, begin+(end-begin)/2)
         + sum_of_squares(x, begin+(end-begin)/2, end);
}  
To use an over-used phrase - see what I did there? We’ve defined the function as the result of that same function on two smaller pieces. This is completely correct mathematically, by the way, the sum of squares of a vector is the sum of the sum of squares of two halves of the vector. Almost. It isn’t correct for the case where end - begin is equal to unity – we can no longer partition the vector. So, in this code example, as with the mathematical example in the sidebar, we need some non-self-referential value (a base case).

With this computation there are several options for a base case. We could stop when the difference between begin and end is unity. We could stop when the difference is sufficiently small. Or, we could stop when we have achieved a certain amount of concurrency (have descended enough levels). In the latter case:
double sum_of_squares(Vector const& x, size_t begin, size_t end, size_t level) {
    if (level == 0) {
        double sum = 0;
        // code that computes the sum of squares of x from begin to end into sum
        return sum;
    } else {
        return sum_of_squares(x, begin, begin+(end-begin)/2, level-1)
             + sum_of_squares(x, begin+(end-begin)/2, end , level-1);
    }
}
Now, we can parallelize this divide and conquer approach by launching asynchronous tasks for the recursive calls and getting the values from the futures. The driver program for this problem is in work/more_warmup/rnorm.cpp.

Complete the implementation for recursive_two_norm_a in work/more_warmup/rnorm.hpp. Your implementation should use the approach outlined above.

Answer the following questions in results/answers.md:

How much parallel speedup do you see for 1, 2, 4, and 8 threads?

What will happen if you use std::launch::deferred instead of std::launch::async when launching tasks?

When will the computations happen? Will you see any speedup?

For your convenience, the driver program will also call recursive_two_norm_b – which you can implement as a copy of recursive_two_norm_a but with the launch policy changed.

General Questions

Answer the following questions in results/answers.md:

For the different approaches to parallelization, were there any major differences in how much parallel speedup that you saw?

You may have seen the speedup slowing down as the problem sizes got larger – if you didn’t, keep trying larger problem sizes.

What is limiting parallel speedup for two_norm (regardless of approach)?

What would determine the problem sizes where you should see ideal speedup? Hint: Roofline model.

Conundrum #1

The various drivers for parallel norm take as arguments a minimum problem size to work on, a maximum problem size, and the max number of threads to scale to. In the problems we have been looking at above, we started with a fairly large Vector and then scaled it up and we analyzed the resulting performance with the roofline model. As we also know from our experience thus far in the course, operating with smaller data puts us in a more favorable position to utilize caches well.

Using one of the parallel norm programs you wrote above, run on some small problem sizes:

$ ./build/work/more_warmup/pnorm 128 256

What is the result? (Hint: You may need to be patient for this to finish.) There are two-three things I would like to discuss about this on Discord:

What is causing this behavior?
How could this behavior be fixed?

Parallel Sparse Matrix-Vector Multiply

Your starter repository has a program work/more_warmup/pmatvec.cpp. This is a driver program identical to matvec.cpp from the midterm, except that each call to mult now has an additional argument to specify the number of threads (equivalently, partitions) to use in the operation. E.g., the call to mult with COO is now

mult(ACOO, x, y, nthreads);  

The program runs just like matvec.cpp – it runs sparse matvec and sparse transpose matvec over each type of sparse matrix (we do not include AOS) for a range of problem sizes, printing out GFlops/sec for each. There is an outer loop that repeats this process for 1, 2, 4, and 8 threads. (You can adjust problem size and max number of threads to try by passing in arguments on the command line.) I have added the appropriate overloads for mult in work/include/matrix_operations_sparse.hpp and work/src/matrix_operations_sparse.cpp. Right now, they just ignore the extra argument and call the matvec (and t_matvec) member function of the matrix that is passed in. There are six total multiply algorithms – a matvec and a t_matvec member function for each of COO, CSR, and CSC. Since the calls to mult ultimately boil down to a call to the member function, we can parallelize mult by parallelizing the member function.

Partitioning Matrix Vector Product

But, before diving right into that, let’s apply our parallelization design patterns. One way to split up the problem would be to divide it up like we did with two_norm:

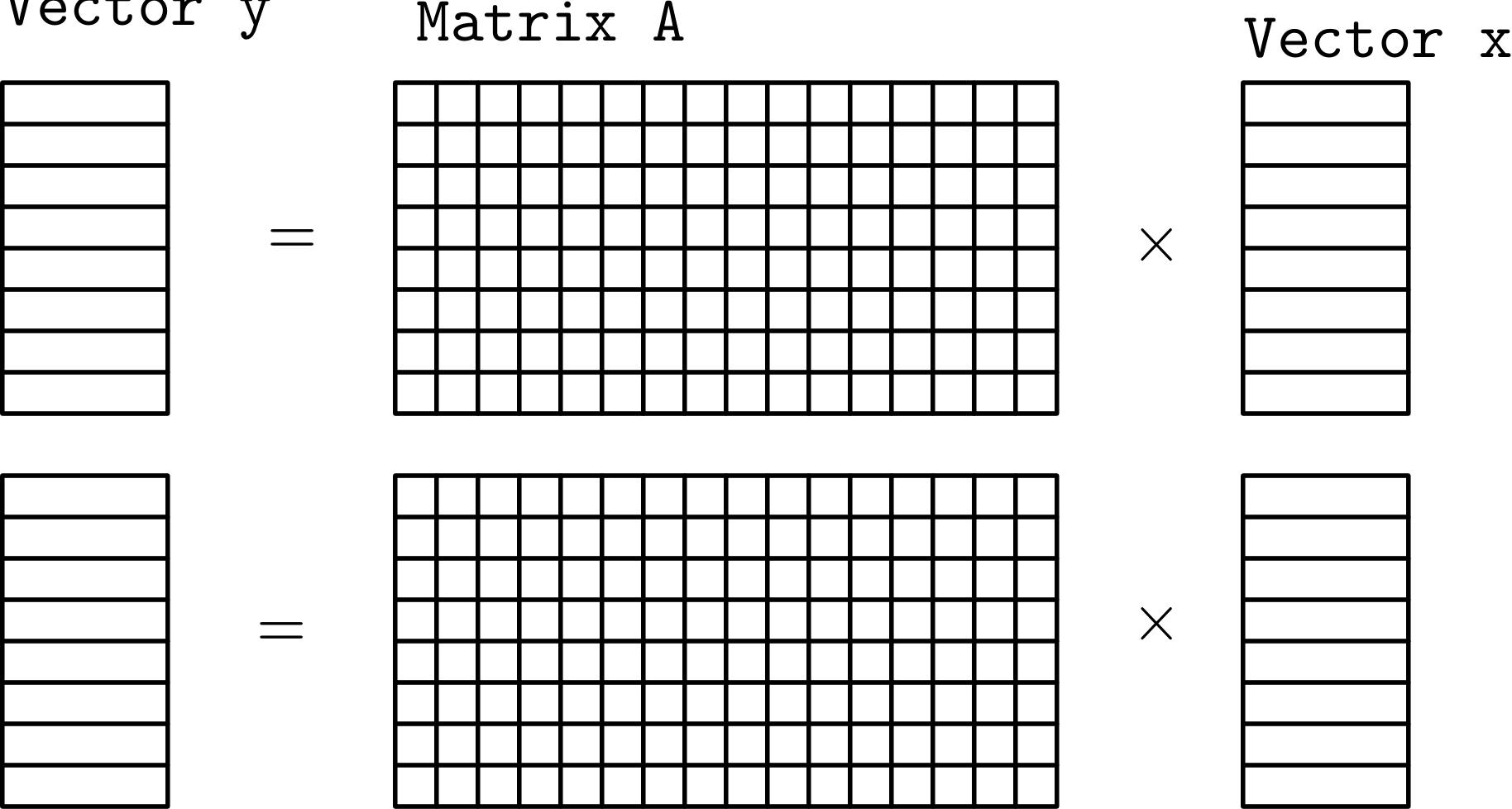
(For illustration purposes we represent the matrix as a dense matrix.) Conceptually this seems nice, but mathematically it is incorrect. Since we are partitioning the matrix so that each task has all of the columns of A we also need to be able to access all of the columns of x – so we can’t really partition x though we can partition y and we can partition A – row wise.

If we did want to split up x, we could partition A column wise but then each task has all of the rows of A so we can’t partition y.

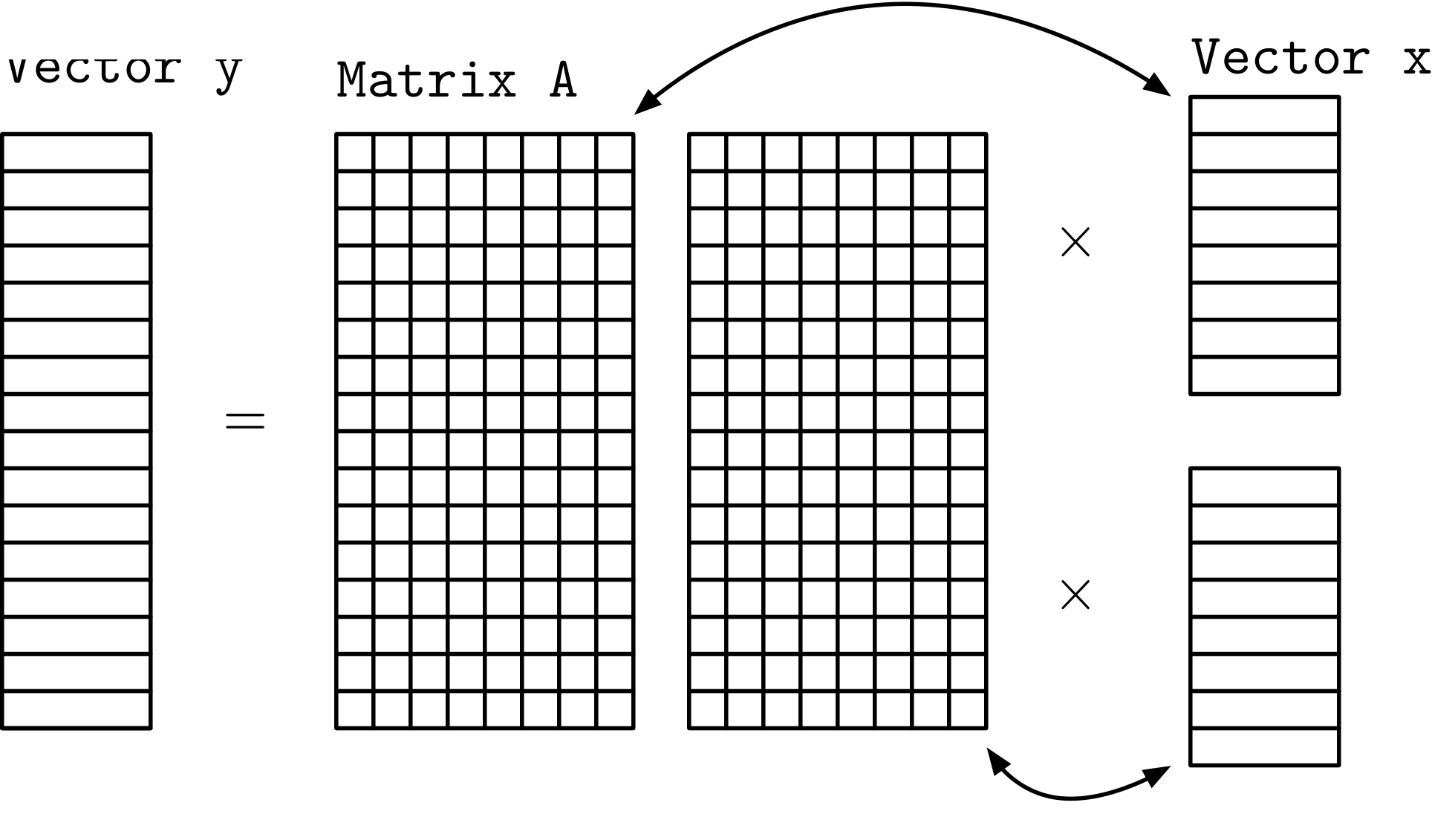
Answers are not required in results/answers.md, but you should think about this:

What does this situation look like if we are computing the transpose product?

If we partition A by rows and want to take the transpose product against x can we partition x or y?

Similarly, if we partition A by columns can we partition x or y?

Partitioning Sparse Matrix Vector Product

Now let’s return to thinking about partitioning sparse matrix-vector product. We have three sparse matrix representations: COO, CSR, and CSC. If you count AOS as well, then we have four sparse matrix representations. We can really only partition CSR and CSC and we can really only partition CSR by rows and CSC by columns. (The looping over the elements in these formats is over rows and columns for CSR and CSC, respectively in the outer loop – which can be partitioned. The loop orders can’t be changed, and the inner loop can’t really be partitioned based on index range.) So that leaves four algorithms with partitionings – CSR partitioned by row for matvec and transpose matvec and CSC partitioned by column for matvec and transposed matvec. For each of the matrix formats, one of the operations allowed us to partition x and the other to partition y.

Answers are not required in results/answers.md, but you should think about this and discuss on Discord:

Are there any potential problems with not being able to partition x?

Are there any potential problems with not being able to partition y?

(In parallel computing, “potential problem” usually means race condition)

Implement the safe-to-implement parallel algorithms as the appropriate overloaded member functions in work/include/CSCMatrix.hpp and work/include/CSRMatrix.hpp. The prototype should be the same as the existing member functions, but with an additional argument specifying the number of partitions. You will need to add the appropriate #include statements for any additional C++ library functionality you use. You will also need to modify the appropriate dispatch function in work/src/matrix_operations_sparse.cpp (these are already overloaded with number of partitions but only call the sequential member functions) – search for “Fix me”.

Answer the following questions in results/answers.md:

Which methods did you implement?

How much parallel speedup do you see for the methods that you implemented for 1, 2, 4, and 8 threads?

Next up: Parallelism